Keywords: Cable Stayed Bridge, Suspension Bridge
1 Introduction
Cable-stayed bridge a
bridge in which the weight of the deck is supported by a number of cables
running directly to one or more towers.
Below
is table of few of the historical cable supported bridges, later on different
parts and types of bridge elements has been discussed in brief. Below we have
table showing major suspension and cable stayed bridge respectively till 2012.
2 Cables
The basic element for all cables to be
found in modern cable supported bridges is the steel wire characterized by a considerably
larger tensile strength than that of ordinary structural steel. Mostly 3-7mm
cylindrical wire is used, typically 5-5.5mm for main cable whereas up to 7mm
diameter used for parallel cable in cable stayed bridge. The wires are
manufactured by the Siemens–Martin process or as electro steel.
2.1 Types of cables:
a. Helical Bridge strands
Fabricated by successive spinning of
layers generally with opposite direction of helix, starting with a straight
core. Smaller pitch uses as compared with 7 wire strands. Strength is reduced
10% due to such configuration i.e. 0.9 fcbd where fcbd is
design stress of a parallel-wire strand of the same wire. Axial tension
increases length for the first time so to act ideally during service before use
these are subjected to overloading of 10-20%(pre-stretching).
b. Locked coil strands
There are two types of twisted wire at
core: round wire in helical pattern and at outer part: Z-shaped wire. Z-locking
makes it less sensitive to the pressure. These are always manufactured in full
length and full cross section.
Parallel wire strands
All wires are straight from end to end. It
had a lot of advantages but due to reeling problem this was used very late for
construction. These are formed in pattern of regular hexagonal, deformed
hexagonal, quasi hexagonal etc.
Parallel wire stay cables
These are more common in cable stayed
bridges than in suspension bridge. This has less integrity than the helical
strand so needs additional support like twisting the steel rope around the
bundle furthermore to give adequate corrosion protection the parallel wire has
to be surrounded by a tube and the void filled with a corrosion inhibitor
(Galvanized). The disadvantage of this is that diameter becomes more and weight
is also increased.
New PWS cables
1990’s variant of parallel wire stay wire
stay cable (slightly twisted) with a long lay to ease reeling and unreeling and
make self-compacting when subjected to axial tension. There seems to be
relationship between tensile force vs twist angle which is shown below in
graph. This is more compact than traditional PWS but has less equivalent
density.
Parallel strand stay cables
In principle composed in same way as
parallel wire stay cable with exception that individual 7 mm wires are replaced
by seven wire strands.
Bar stay Cables
Hardly used now and they contained 7-10
round steel bars each diameter 26.5mm,32mm or 36mm made of steel of yield
stress 1080MPa and tensile strength of 1230MPa with fabrication length 12m then
joined by threaded couplers. Bundled and placed in steel tube and grouted with
cement.
Multi-strand stay cable
These are used for large cable section
requirement and made of several helical strands in both cable stayed and
suspension bridges.
Parallel-wire suspension bridge main
cables

3 Cable System
3.1 Introduction
The selection of cable system is most decisive step in
design of cable supported bridges as this further dictates the amount of
material as well as type and maximum of loading that structure will efficiently
bear.
Quantity of steel:
Only three cable systems will be discussed: a)
Suspension system b) Fan system & c) Harp system.
For pure cable systems (with all elements as cables in
tension), subjected to uniform load, the theoretical cable steel quantity is
the same for the suspension system, and the harp system with equal horizontal
force. The formula given below is based on consideration of equal horizontal
force and also the inclination of cable has not been included. Furthermore, in
the formula the height(h) for the suspension system and fan system is same
while the harp system it is higher. This is just for understanding the
characteristics of the cable system but of no practical use as the pure cable
system is never used in cable stayed bridges.
Qcb = Theoretical quantity of cable steel, P = Vertical forces acting on
constantly spaced hangers, h
= Height of the system of cable chosen, λ = Distance successive hangers, γcb = Density of
the cable material, fcbd
= Design stress, n
= Number of cable elements
The harp system shows (in fig) the smallest quantity
and the suspension system the largest. The h/l values used in actual structures
are smaller than these values as the optimization must take into account the
material of the pylon. For the suspension system stiffness requirements furthermore
prescribe h/l values in the interval from 0.08 to 0.12.
If the
suspension system is changed to a fan system with the same height and with all
elements as cables in tension the cable steel quantity remains the same, as
stated in the previous theorem. But by replacing the horizontal cable elements
by the deck, the cable steel quantity is reduced to 69%. If finally, the pylon
height is increased to one-fifth of the span length, then the theoretical cable
steel quantity is reduced further to only 46%. Although the optimum height (hopt= λ) for the for minimum steel theoretically gives the value of inclination
to be 450 but while considering pylon contribution the more
realistic value for cable inclination which is also economical is 300 at
hopt= λ/√3. The case with hopt= λ has minimum deflection too which is 15% more in the case with hopt= λ/√3.
3.1.1 Stability of Cable system:
In traditional suspension bridge cable system may be
represented by the structural elements made of cables but parts of deck and
pylon should be added resisting axial forces induced by the horizontal or
vertical components of forces at the anchor points.
The cable system further can have 3 cases with above assumptions:
·
A cable system stable of the first order. In this
system, equilibrium can be achieved without assuming any displacement of the
nodes.
·
A cable system stable of the second order. In this
system, equilibrium can only be achieved with nodes displaced under the action
of the external load.
·
An unstable cable system. In this system, equilibrium
cannot be achieved by the cable system itself.
By analysing the different cases and system we can
conclude following:
·
The fan system is a system stable of the first order
but if the overall dimensions (ratio between side span and main span) are
chosen without respect to the relative intensity of the traffic load, an almost
complete release of the anchor cable tension might occur, and in that case the
idealized cable system will become unstable. Thus, this will need anchor cable
to restore its stability.
·
The traditional suspension system is stable of second
order, this will remain stable for loading cases.
·
The harp system is an unstable system but the fact that
harp system is unstable system does not imply that the total structural system
of the bridge is unstable, as the flexural stiffness of the deck and pylon will
add the stability.
·
In the total structural system of the bridge the cable
system only forms one part, and the total system can therefore very well show a
satisfactory load-carrying capability, even if the cable system is unstable.
However, it will be found that the global stiffness and the load-carrying
efficiency of the total system depend to a very large extent on the cable
system and especially if the deck is slender and has a modest flexural
stiffness.
3.2 Suspension system
In the traditional earth anchored suspension bridge
each main cable is supported at four points: at the two anchor blocks and on
the two pylon tops. The supporting points at the anchor blocks can generally be
assumed to be completely fixed both vertically and horizontally, whereas the
supporting points at the pylon tops often are represented best by
longitudinally movable bearings (due to the horizontal flexibility of the
slender pylon legs).
The main cable geometry can then be expressed by the
following equations,
where Ma(x), Mm(x), and Mb(x)
are the moments of simply supported beams with lengths la, lm,
lb subjected to the total dead load of main cable, hangers, and
deck.
where Mm(lm/2) is the simple
moment at the main span centre and hc - hD/2 the cable
sag at midspan.
3.2.1 Preliminary cable dimensions
In the process of designing a suspension bridge it is
advantageous to be able to make a quick, preliminary calculation of the cable
dimensions.
3.2.2 Quantity in the Pylon
When optimizing the superstructure of a suspension
bridge it is essential to take into account the variation in the quantities of
the pylons, whereas the quantities (per unit length) of the deck often remain
constant and consequently only influence the dead loads ga and gm
to be applied to the cable system.
Apart from above qualities of material may differ for
different conditions like height of pylon and cable material can be optimised
owing to sag ratio and unit rate of materials. Nevertheless, the size also
plays the significant role on the quantity of the materials required for the
chosen system of bridge.
3.3 Fan system
In cable stayed bridges the fan system has become the favourite
cable system due to its efficiency and the degree of freedom regarding
geometrical adaption.
3.3.1 Anchor cable
The anchor cable connecting the pylon top to the end
support plays a dominant role in the achievement of stability in the cable
system.
The dimensions of the system is influenced by the
stress ratio, above graph shows the variation of the critical side to main span
ratio (la/lm) with the traffic to dead load ratio (p/g)
and the stress ratio (Kac).
3.3.2 Preliminary cable dimensions
A preliminary design of stay cables can be based on
the same assumptions as those applied for the hangers of the suspension bridge.
3.3.3 Quantity in the pylon
The quantity of the pylon is
However, for the cable steel there is a difference due
to the higher cost of the corrosion protection and the large number of heavy
sockets in a cable stayed bridge.
3.4 Harp system
An unstable cable system, so that the flexural
stiffness of the deck and the pylons must be taken into account to achieve
equilibrium. The stability of bridges with harp-shaped cable systems can be
achieved in principle by two basic structural systems: either by applying a
stiff deck and a slender pylon, or by a slender deck and a stiff pylon.
3.4.1 Dead load geometry
To avoid unnecessary bending from dead load, the
geometry of the harp system is often chosen so that the dead load is balanced
completely. For a constant dead load this simply leads to a symmetrical
arrangement of the stays in relation to the pylon. For a difference between the
main span dead load gm and the side span dead load ga as indicated
in Figure below the balance is obtained if the horizontal component Hab
of stay cable AB is equal to the horizontal component Hbc of stay cable
BC:
Consequently, the distance between the cable anchor
points shall be inversely proportional to the square root of the dead load
intensity to obtain balance.
3.4.2 Interior support
The disadvantages of the harp system due to the
unstable cable system can be completely eliminated if intermediate supports are
added under all cable anchor points in the side spans, as indicated in Figure below.
The cable system will then change to a system that is stable of the first order.
3.4.3 Preliminary cable dimensions
In the preliminary design process the cross section of
the stay cables can be determined by equations similar to those found for the
fan system.
3.4.4 Quantity of cable steel
3.4.5 Quantity of the pylon
4 Deck
The deck is the structural element subjected to the
major part of the external load on a cable supported bridge. This is because
the total traffic load is applied directly to the deck, and in most cases both
the dead load and the wind area are larger for the deck than for the cable
system. Immediately the deck must be able to transfer the load locally whereas
it will receive strong decisive assistance from the cable system in the global
transmission of the (vertical) load to the supporting points at the main piers.
4.1 Flexural stiffness in the vertical direction
Action 1: to carry the load locally between cable
anchor points. Action 1 of the deck therefore corresponds to the action of
stringers in a truss bridge where the load on the bridge floor has to be
carried to the cross beams at the nodes of the main trusses.
Action 2: to assist the cable system in carrying the
load globally. Action 2 of the deck is found in bridges with unstable systems,
as has been described, e.g. for the harp system. Here the deck must be able to
carry a part of the traffic load not only between adjacent cable anchor points
but also between the main supports of the bridge.
Action 3: to distribute concentrated forces. The
deck’s ability to distribute concentrated forces (Action 3) will be utilized
primarily in bridges with a large number of cables supported points as found in
both the suspension bridges and cable stayed bridges at the multi-cable system.
4.2 Flexural stiffness in the transverse direction
The transmission of lateral forces from wind (or an
earthquake) acting on the deck and on the cable, system induces bending about a
vertical axis. Change from simply supported spans to continuous spans
significantly decreases the lateral deflection of the deck, the load carried by
the cable system will be reduced. Under lateral wind load the stay cables will
swing sideways to make the plane of the catenary coincide with the direction of
the resultant force from the cable dead load gcb and the wind load ucb,
as illustrated in Figure below. Consequently, the wind load will be transferred
to the cable anchor points in the same way as the dead load. Therefore, lateral
forces equal to half the total wind force 1/2ucbc will be induced at
the deck and the other half at the pylon.
4.3 Torsional stiffness
The torsional stiffness (and strength) required in the
deck depend to a large degree on the amount of torsional support offered by the
cable system. If the bridge has single cable plane then the torsional stiffness
of the deck is significant but if the bridge has two cable planes then the
torsional stiffness of deck is not important yet deck with torsional stiffness
is favourable for the overall stability.
4.4 Supporting Conditions
The interaction between the deck, the cable system and
the pylons in the transmission of vertical and horizontal loads is decisively
influenced by the choice of the supporting conditions for the deck. In the
conventional three-span suspension bridge the deck often consists of three
individual girders with simple supports at the pylons and the end piers (anchor
blocks). Generally, the end pier supports will be longitudinally fixed whereas
all other supports are made longitudinally movable, so that all expansion will
take place in the two joints at the pylons. In bridges with large longitudinal
forces a further restraint of the main span deck might be desirable. Such a
restraint could be accomplished in the following ways:
(1) By applying a fixed support at one of the pylons.
(2) By connecting the deck and the main cable through
a central clamp at midspan.
(3) By centering the main span deck by a device.
(4) By installing shock absorbers at the pylons,
allowing slow thermal movements but excluding movements from short-term loading
such as braking forces.
In self-anchored cable stayed bridges the maximum
axial forces in the deck occur at the pylons, and it is therefore not possible
to make the deck discontinuous at these points. Only at midspan in the region
between the two top cable anchors points will it be possible to arrange an
expansion joint, as the axial force is zero at that location.
5 Pylons
In principle, the pylon is a tower structure, but in
contrast to a free-standing tower, where the moment induced by the horizontal
loading (drag) from wind dominates the design, the most decisive load on a
regular pylon will be the axial force originating from the vertical components
of the forces in the cables attached to the pylon.
Relation between the relative pylon weight Qpl/Npt
and the pylon height hpl for different stress-to-density ratios is
shown below in the plot.
If the force transferred from the cable to the pylon
is acting in the plane of ABCD (the plane formed by centroidal axis of pylon
and deck) as shown above then the force on the pylon will still act along the B
but if there is presence of lateral load then the deck will deform and there
will be eccentricity to the force on the pylon and direction will shift toward
B’. Depending upon the system of the bridge structure the action of force on
the pylon and direction differs.
The pylons depending upon the fixity of base can have
different cases and similarly may have different action of force transfer
offering unique design conditions that allows certain pros and cons.
6 Cable anchorage and connection
The proper cable anchorage and connection between
pylon, deck and cables is very important and should be worked out carefully
with details. For in situ cables built up from individual wires at the site,
e.g. parallel-wire cables erected by the air-spinning method, the anchoring is
generally established by looping the wires around a strand shoe. For
prefabricated strands the most common way of anchoring is by socketing the ends
of the strands. The
fact that the high strength of the wire is achieved during the cold drawing
process implies that a strength reduction might appear if the metallic alloy
requires a high pouring temperature. Below (left) is the figure of the strand
shoe for anchoring stands erected by the air-spinning method. Another plot
shows the influence of poring temperature on the ultimate strength σu
of the wire.



























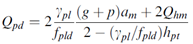







0 Comments